El perímetro y el área son dos de las propiedades más importantes de figuras bidimensionales. El perímetro define a la distancia alrededor de los límites de la figura, mientras que el área indica la región ocupada por la figura. Estas propiedades son usadas para describir a la figura y realizar diferentes cálculos. El perímetro y el área son aplicables a cualquier figura cerrada sin importar si es regular o irregular.
A continuación, conoceremos las fórmulas del perímetro y del área de algunas figuras bidimensionales más comunes. Luego, usaremos estas fórmulas para resolver algunos ejercicios.
¿Qué es el área?
El área es definida como la región ocupada por una figura en el espacio bidimensional, es decir, el área es el espacio cubierto por la figura. El área de cualquier figura depende de sus dimensiones y de sus propiedades.
Esto significa que las fórmulas usadas para calcular el área, varían dependiendo en la forma de la figura. Por ejemplo, la fórmula para calcular el área de un triángulo es diferente a la fórmula para calcular el área de un cuadrado.
Si es que dos objetos tienen la misma forma, sus áreas no serán las mismas necesariamente. Para que el área de dos objetos sea la misma, tanto sus formas como sus dimensiones deben ser las mismas.
Por ejemplo, supongamos que tenemos a un rectángulo con ancho A y longitud B y tenemos a un segundo rectángulo con ancho C y longitud D. Para que el área de los rectángulos sea la misma, debemos tener A=C y B=D.
¿Qué es el perímetro?
El perímetro de una figura es definido como la distancia total alrededor de la figura. El perímetro puede ser considerado como la longitud total de una figura si es que esta fuera expandida en una forma lineal.
El perímetro de figuras que tienen diferentes formas pude ser el mismo dependiendo en las dimensiones de las figuras. Por ejemplo, si es que construimos a un círculo con un alambre de cobre, el mismo alambre de cobre puede ser usado para construir a un cuadrado, el cual tendrá lados con igual longitud.
La fórmula del perímetro dependerá en la forma de la figura y en el número de lados que tiene la figura.
Fórmulas del perímetro y área de varias figuras
Existen una gran cantidad de figuras geométricas, las cuales tienen diferentes fórmulas para calcular el perímetro y el área. Sin embargo, las figuras más comunes son el cuadrado, el triángulo, el rectángulo y el círculo.
Perímetro y área de un rectángulo
Un rectángulo es una figura en la que todos sus ángulos internos miden 90° y en la que sus lados opuestos son iguales.
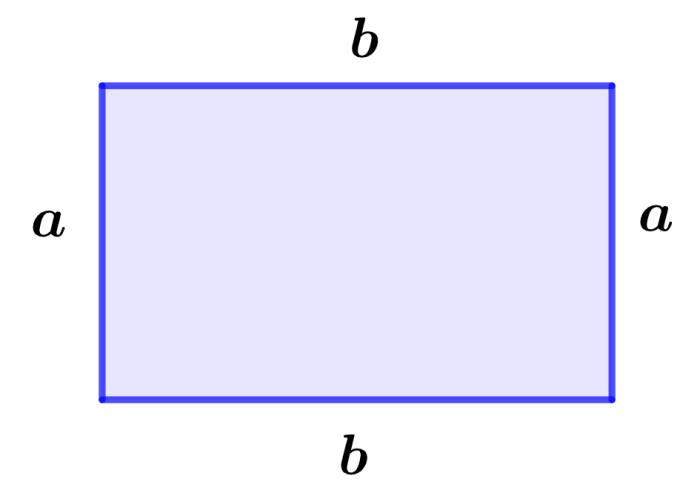
Perímetro de rectángulo = 2(a+b)
Área de rectángulo = a×b
en donde, a es el ancho del rectángulo y b es su longitud.
Perímetro y área de un cuadrado
Un cuadrado es una figura que tiene cuatro lados iguales y en la que sus cuatro ángulos internos miden 90°. Un cuadrado es un tipo especial de rectángulo.
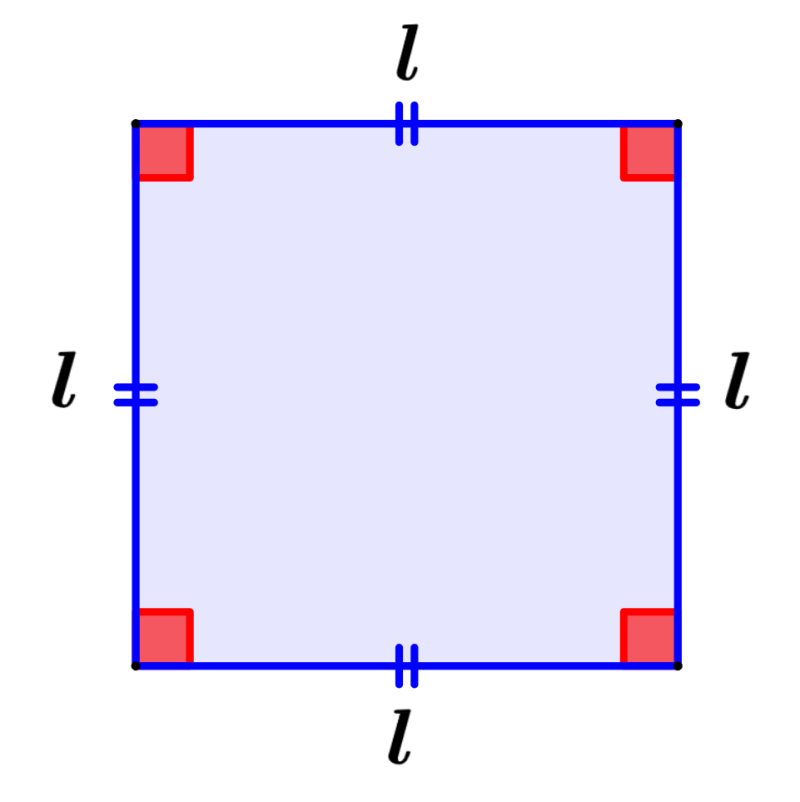
Perímetro de un cuadrado = 4l
Área de un cuadrado = l²
en donde, l es la longitud de uno de los lados del cuadrado.
Perímetro y área de un triángulo
Un triángulo es una figura con tres lados. Dependiendo en las características de sus lados, el triángulo puede ser equilátero, isósceles o escaleno. Sin embargo, las fórmulas para calcular el perímetro y área de los diferentes tipos de triángulos son las mismas.
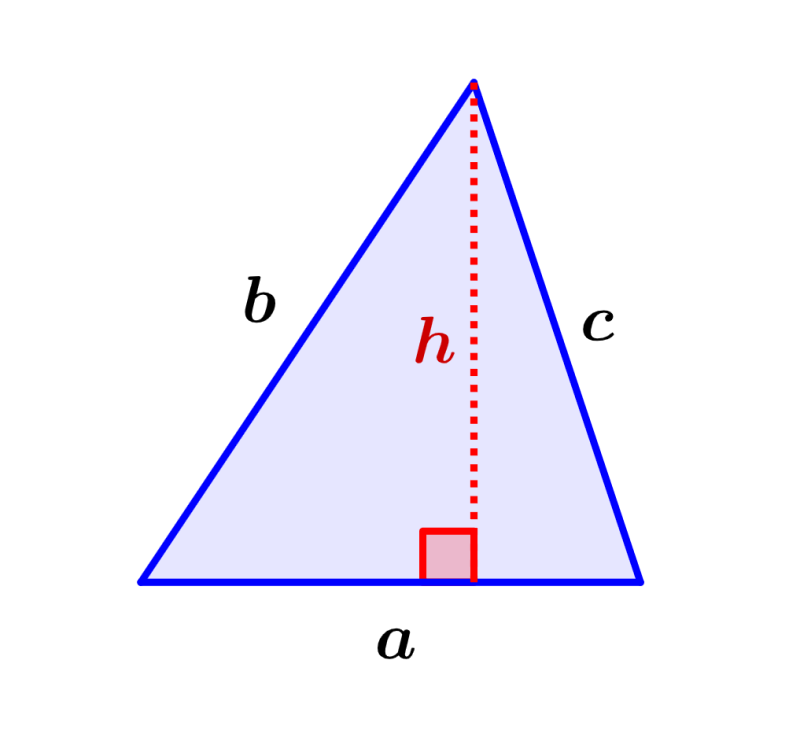
Perímetro de un triángulo = a+b+c
Área de un triángulo = ½ha
en donde, a, b, c son las longitudes de los tres lados del triángulo, h es la altura y a es la base del triángulo.
Perímetro y área de un círculo
El círculo es una figura que tiene una forma completamente redonda. Tanto el perímetro como el área son calculados usando el radio, el cual es la longitud desde el centro del círculo hasta un punto en su circunferencia.
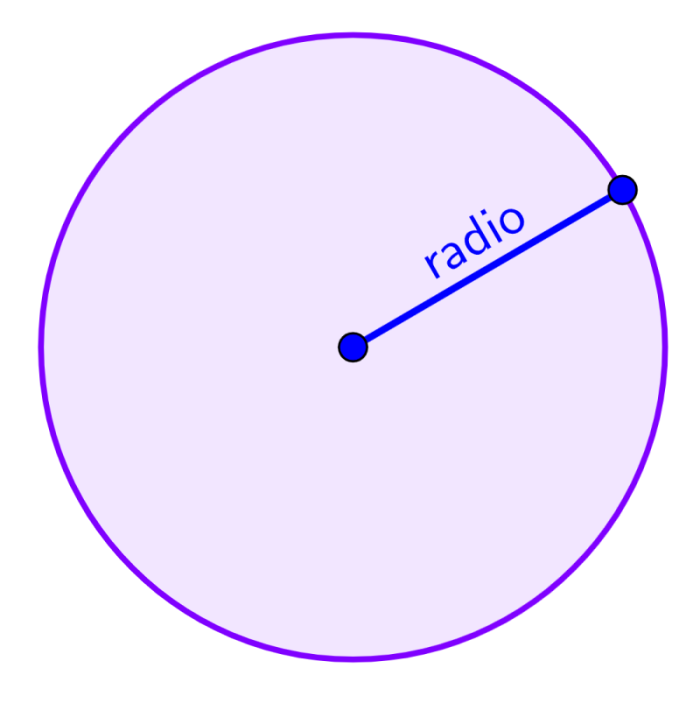
Perímetro del círculo = 2πr
Área del círculo = πr²
en donde, r es el radio del círculo y π es una constante numérica que tiene un valor de 3.1415…
Tabla de fórmulas de perímetro y área
| Figura | Área | Perímetro |
| Círculo | A = πr² | P = 2πr |
| Triángulo | A = ½ bh | P = a+b+c |
| Cuadrado | A = l² | P = 4l |
| Rectángulo | A = ab | P = 2(a+b) |
| Paralelogramo | A = bh | P = 2(a+b) |
| Polígono regular | A = ½ nla | P = nl |
Círculo: r es el radio y π es la contante igual a 3.1415…
Triángulo: b es la base, h es la altura y a, b, c son las longitudes de los lados.
Cuadrado: l es la longitud de un lado.
Rectángulo: a es la longitud del ancho y b es la longitud de la base.
Paralelogramo: b es la longitud de la base y h es la longitud de la altura.
Polígono regular: n es el número de lados del polígono regular, l es la longitud de uno de los lados y a es la longitud de la apotema. La apotema es igual a la distancia desde el centro hasta uno de los lados
Comentarios
Publicar un comentario